Intro
I love chess. I play chess all the time (Steinshark on Lichess). The problem is I suuuuuck at chess. However. I do not suck at programming. Or machine learning. Or training chess bots, as it turns out ;)
AlphaZero exploded onto the scene in 2017, shaking up the chess content scene and finally allowing GothamChess to fit magnus AND ai into a single thumbnail. Claims of blowing stockfish out of the water were rampant, if not a bit misplaced after some simmering down of the scene. In either case, the rise of a self-learning bot was awesome. I wanted to do it to. Enter the chess project.
Phase 1 - Deciphering the Paper
It turns out that the AlphaZero algorithm isn't easy to understand. That kinda makes sense... else we would have just done it earlier than a few years ago. Civilization has finally made it to the fertile valley of both compute and human creativity. Reinforcmenet learning takes both of those things. A lot of them. Like seriously a lot of them. But in either case, I had enough of each - at least Nvidia and DeepMind did. So I'll take the piggy back on the way up.
Onto the algorithm... The real novel idea here was departing form the traditional wisdom of the alpha-beta pruning trees that DeepBlue used to defeat Kasparov. This was the conventional wisdom chess bots had been using since time immemorium (the last 50 years). Instead, the team decided to use a Monte Carlo Tree search guided by a neural network. Lets break this down...
The Monte Carlo Tree Search
A Monte Carlo simulation is one in which we have a problem that we know how to simulate but not how to solve for directly. Heres an example: We want to compute a value for pi. Well, it's not exactly straightforward to do that. It is extremely easy to randomly place points on a cartesian coordinate grid. And its easy to calculate \(x^2 + y^2 < r^2\). If we place enough points, we can estimate - based on the ratio - the area of a circle of radius r. Then we just solve \(A = \pi r^2\) for \(\pi\)!
Easy to observe, hard to calculate directly.
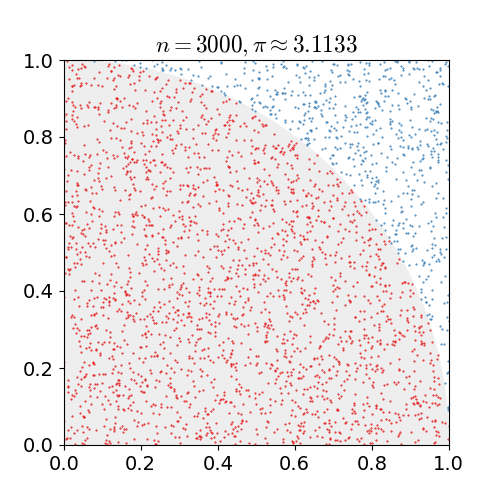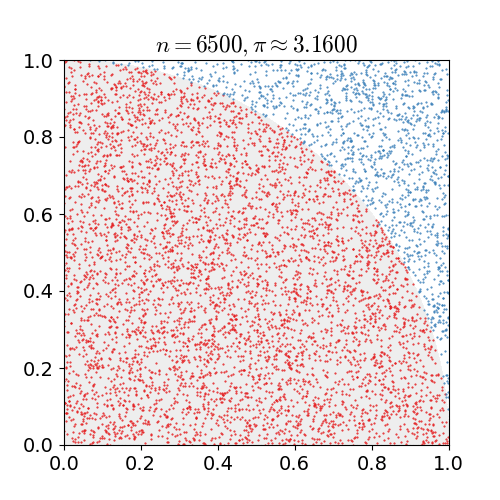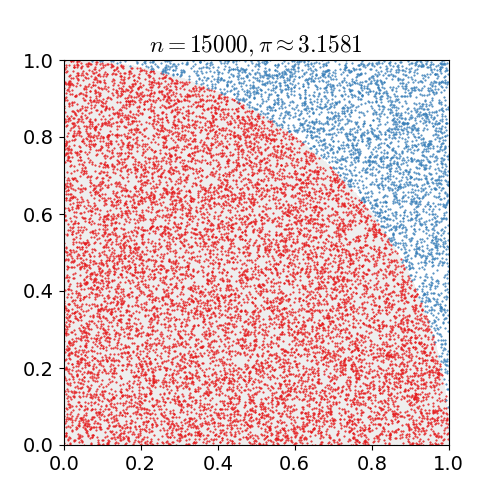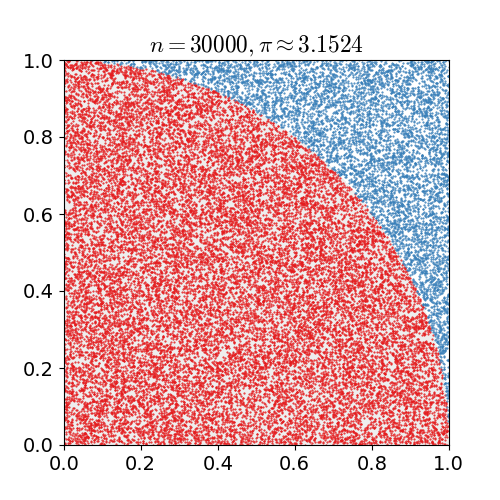
Monte Carlo simulation to estimate the value of pi.
Now we just need a clever way to apply that to games. Lets say we're playing tic-tac-toe. To monte-carlo search tic-tac-toe, I'll just make a tree of all possible move combinations starting from an empty board. Play out dozens of random games, and well see certain branches have more cumulative wins than others. These are the better moves. And thus, without any sophsticated methods we have devised a game plan from simply observing simluated actions.
The Neural Network
Unfortunately, theres more nodes in the Chess game tree than there are atoms in the universe. It would seem we cannot just observe making all these moves. Enter the neural network. Instead of trying to brute force all the moves, lets try to observe just the ones we think make sense - with a little exploration. A neural network will help guide us down paths that would most likely yield good results for us. THis happens in 2 ways: with poth a policy and a value.
The Policy \(\pi\)
The policy aims to give us the likelihood that we should take move \(a|S\) (read: "a" given S), where a is an action (a move) and S is the game state (current position, who's turn it is, castling rights). Our motivation is to train the network such that "good moves" (whatever that means!?) get higher probabilities. This allows us to immediately cue our search down good moves without doing any other work.
The Value \(v\)
In addition to the policy, the network will also yield a value for the given board state. If \(v=1\), then the model thinks white is winning here. \(v=-1\) means black ought to win, and 0 is a draw. The value helps give us a way to assign scores to a branch. Given how sparse outcomes are in chess (only 1 per game!), we need a heuristic on the way down.
Check for More Next Time!
Next iteration, we'll check out how the monte carlo algorithm utilizes the policy and the value to search a given board state. We'll also find out how we decide which moves are "good" using this algorithm!