Intro
I love chess. I play chess all the time (Steinshark on Lichess). The problem is I suuuuuck at chess. However. I do not suck at programming. Or machine learning. Or training chess bots, as it turns out ;)
AlphaZero exploded onto the scene in 2017, shaking up the chess content scene and finally allowing GothamChess to fit magnus AND ai into a single thumbnail. Claims of blowing stockfish out of the water were rampant, if not a bit misplaced after some simmering down of the scene. In either case, the rise of a self-learning bot was awesome. I wanted to do it to. Enter the chess project.
Phase 2 - Implementing the Code
Coding is the fun part - until its time to debug. And there was a hell of a lot of debugging this code. There are so many traps when performing tree search.
Onto the algorithm... The real novel idea here was departing form the traditional wisdom of the alpha-beta pruning trees that DeepBlue used to defeat Kasparov. This was the conventional wisdom chess bots had been using since time immemorium (the last 50 years). Instead, the team decided to use a Monte Carlo Tree search guided by a neural network. Lets break this down...
The Monte Carlo Tree Search
A Monte Carlo simulation is one in which we have a problem that we know how to simulate but not how to solve for directly. Heres an example: We want to compute a value for pi. Well, it's not exactly straightforward to do that. It is extremely easy to randomly place points on a cartesian coordinate grid. And its easy to calculate \(x^2 + y^2 < r^2\). If we place enough points, we can estimate - based on the ratio - the area of a circle of radius r. Then we just solve \(A=\pi r^2\) for \(\pi\)!
Easy to observe, hard to calculate directly.
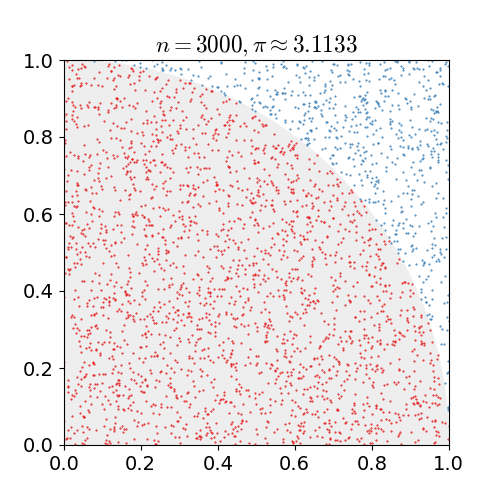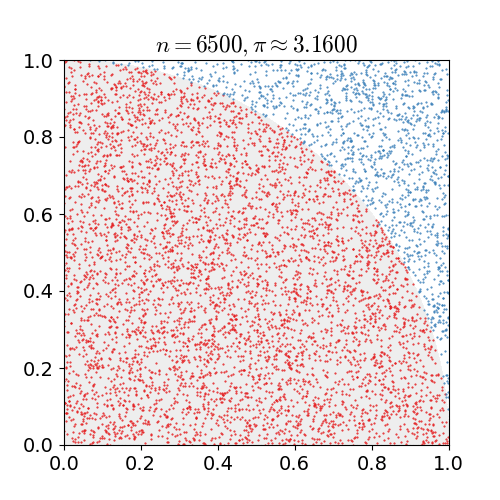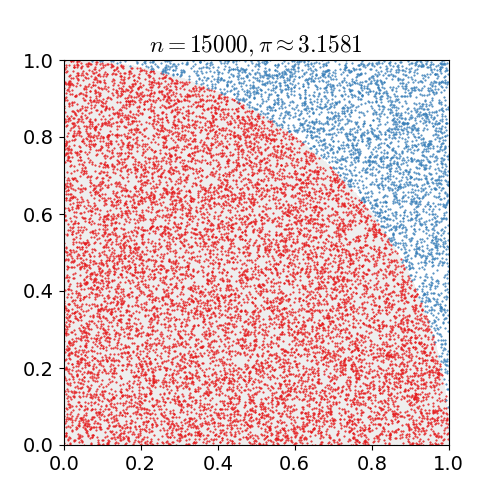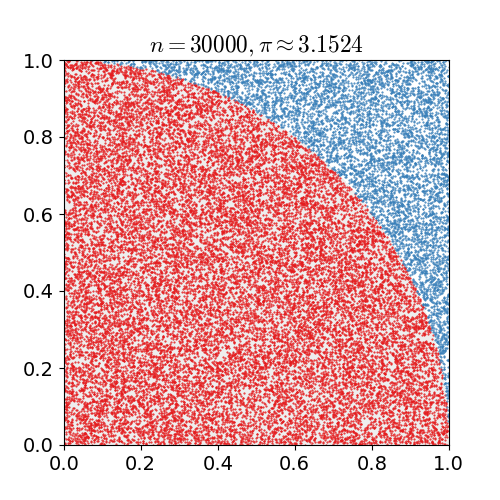
Monte Carlo simulation to estimate the value of pi.
